A/B Testing - Lý thuyết cơ bản và cách áp dụng
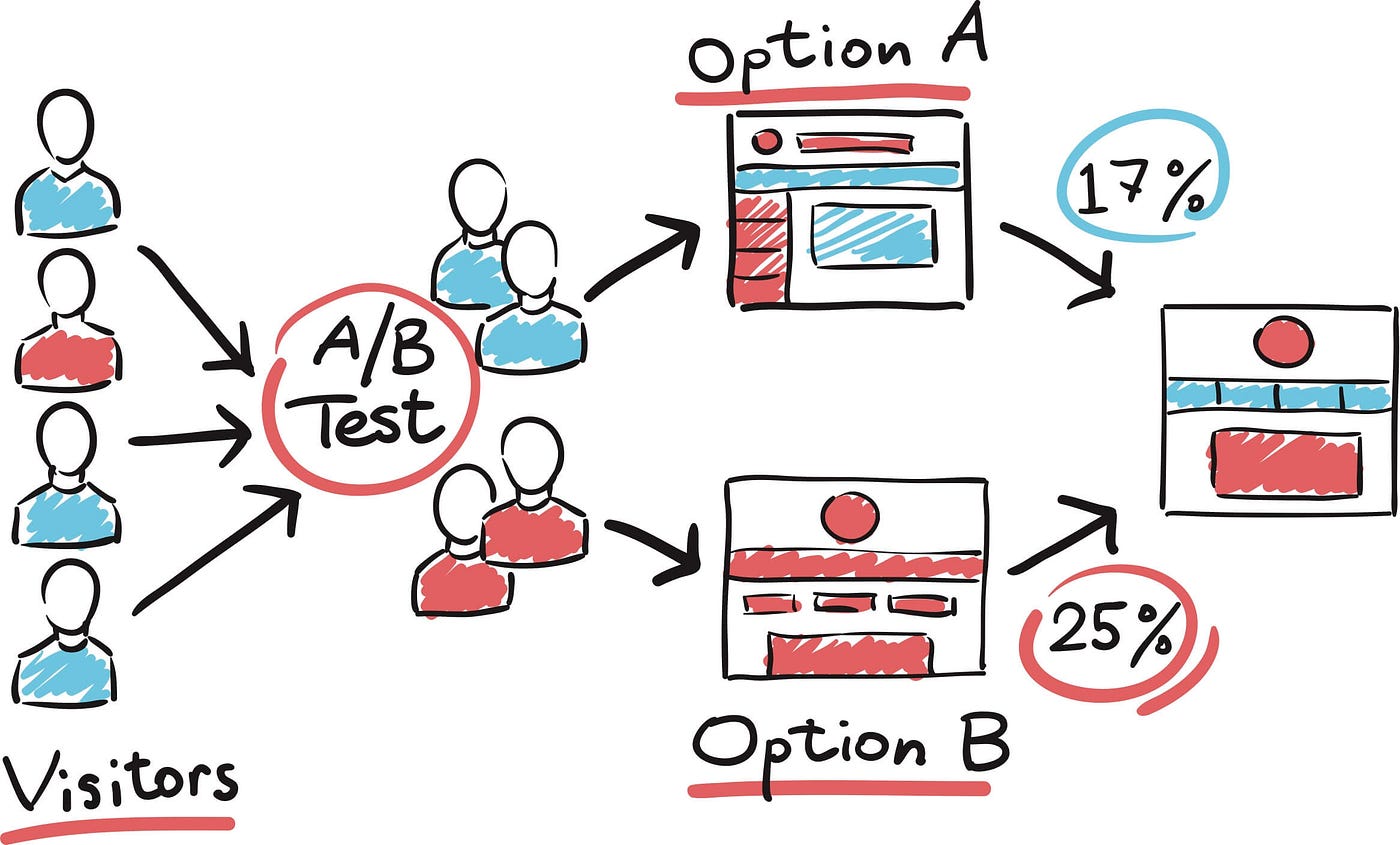
Tại sao chúng ta cần A/B Testing
Dưới góc nhìn của chúng ta, hầu hết các sự kiện trong cuộc sống đều có tính ngẫu nhiên. Tính ngẫu nhiên này có thể là việc quan sát của chúng ta bị hạn chế, hoặc bản chất của việc đó là ngẫu nhiên. Để rõ hơn phát biểu này, mình sẽ đưa ra 2 ví dụ sau:
Ví dụ đầu tiên để minh họa tính ngẫu nhiên là do việc quan sát của chúng ta bị hạn chế.
- Giả sử mình muốn tính vị trí sau 3 giây của hòn đá lăn trên một con dốc. Vì hạn chế của việc đo đếm các yếu tố tác động đến hòn đá như độ dốc, lực cản, hình dáng con dốc mà mình chỉ có thể tính toán được vị trí tương đối chính xác của hòn đá mà thôi. Vị trí của hòn đá sau 3 giây có thể nằm ở vị trí xung quanh vị trí mà mình ước lượng. Nếu mình có khả năng đo đếm các yếu tố ảnh hưởng chính xác tuyệt đối thì mình có thể tính toán vị trí chính xác theo các quy tắc vật lý. Do đó, vị trí của hòn đá dưới góc nhìn của một nhà quan sát bình thường có tính ngẫu nhiên.
Ví dụ tiếp theo là minh họa bản chất của việc đó là ngẫu nhiên. - Theo mình được biết thì ở thế giới lượng tử, hành vi của hạt nguyên từ và hạ nguyên tử bị ngự trị bởi sự ngẫu nhiên, sự ngẫu nhiên đến từ bản chất của chúng, chứ không phải là do việc quan sát của chúng ta bị hạn chế như ví dụ ở trên. Nguyên lý tất định Heisenberg mô tả rằng một số thuộc tính vật lý như vị trí và vận tốc không thể đồng thời mô tả chính xác dẫn đến kết quả quan sát không tất định. Ví dụ như, khi chơi bóng bàn, để có thể chơi trò này, chúng ta cần biết vị trí và tốc độ của quả bóng. Từ đó mới phán đoán được nên hành xử như thế nào tiếp theo. Nếu biết vị trí mà không biết vận tốc thì làm sao mà đánh lại chớ. Cái sự ngẫu nhiên này đến từ bản chất của các hạt. Kì lạ nhỉ. Thế giới vi mô là nền tảng để cấu tạo nên thế giới vĩ mô. Tuy nhiên ở thế giới vi mô, các hạt lại có bản chất ngẫu nhiên, nhưng ngược lại ở thế giới vi mô, hành vi của các vật lại được mô tả tất định theo nguyên tắc vật lý. Cái bản chất ngẫu nhiên lại tạo nên cái tất định(1).
Dưới góc độ của mình (chúng ta), việc ngẫu nhiên cho dù đến từ bản chất của sự việc hay do hạn chế quan sát, thường không quan trọng, cái chúng ta cần là công cụ để xem xét, đánh giá, so sánh giữa các sự kiện này.
Quay lại với các vấn đề thực tế của chúng ta, thông thường trong các công ty có phát triển sản phẩm như Zalo, Tiki, Momo, …, những ứng dụng của công ty này thường được phát triển lên từ từ, được thêm nhiều tính năng mới, cải thiện tính năng cũ, cải thiện tốc độ phản hồi. Việc bổ sung, cải thiện những tính năng này là hành động chủ quan, có thể làm cho ứng dụng tệ đi hoặc tốt hơn theo nghĩa nào đó ví dụ như ít hoặc nhiều người sử dụng app hàng ngày, ít hoặc nhiều giao dịch. Do đó, chúng ta cần có cách nào đó để kiểm tra xem liệu tính năng mới đó có thực sự tốt hơn như chúng ta nghĩ hay không?
Một phương pháp kiểm tra đơn giản và không chính xác.
Để giải quyết câu hỏi liệu tính năng mới có thực sự tốt hơn hay không? Chúng ta thường nghĩ đến phương pháp kiểm tra sai lầm như sau: Cứ mở tính năng mới cho tất cả khách hàng sử dụng, sau đó quan sát xem liệu các chỉ số như số khách sử dụng hằng ngày có tăng hay không, (và các chỉ số quan trọng khác tùy mô hình kinh doanh). Nếu thấy tăng thì chúng ta bảo là tốt hơn, và cứ thế tự tin rằng mình đang làm điều tốt đẹp.
Phương pháp này tuy sai, nhưng lại đơn giản nên hầu như ai cũng nghĩ được và vì thế nên lại thường được sử dụng (vì người đó không biết sai ở chỗ nào). Nhưng mình nhấn mạnh lại một lần nữa là phương pháp này sai vì những vấn đề không được giải quyết sau:
- Trong thời gian bạn chạy tính năng mới, nhưng yếu tố khác tác động vào làm tăng chỉ số mà bạn đang đo. Ví dụ như bạn đang kiểm tra xem giao diện mới có làm tăng lượt click vào sản phẩm so với giao diện cũ hay không thì bộ phận khác của công ty tăng tiền quảng cáo, tạo ra các mã giảm giá, khuyến mãi cho khách hàng thì có thể chỉ số bạn đang theo dõi cũng tăng theo mặc dù cái giao diện mới chả tạo ra thêm lượt click so với cái giao diện cũ, hoặc các yếu tố ngoài xã hội như dịch bệnh, thời tiết, chính sách nhà nước tác động vào làm tăng hoặc giảm chỉ số đó. Tóm lại có quá nhiều yếu tố khác tác động vào đúng lúc mà bạn đang kiểm định tính năng mới làm cho việc tăng hoặc giảm chỉ số theo phương pháp này không đáng tin cậy.
Hậu quả của việc các chỉ số thống kê không đúng là chúng ta không có có sở đánh giá mức độ cải tiến, chọn nhầm các tính năng tệ hại thay vì tốt thực sự, những ý tưởng kì lạ được hoan nghênh.
Chiến lược ABtest ngây thơ - Cứ nghĩ là AB Test, những lại không phải !
Chúng ta cứ nghĩ rằng AB Test là việc chia tập khách hàng thành 2 tập baseline và variant theo cách ngẫu nhiên có kích thước tương đương nhau. Rồi chạy thí nghiệm, tập baseline thì vẫn giữ model gốc, còn tập variant thì chạy model cải tiến. Rồi sau đó, chỉ cần đơn giản là so sánh các chỉ số business quan trọng trên 2 tập đó là xong, nếu thấy tập variant có giá trị tốt hơn thì chứng tỏ model cải tiến tốt hơn thật, ngược lại thì model cải tiến tệ hơn.
Điều này là một sự sai lầm!
Để hiểu tại sao lại sai lầm, mình sẽ chuyển sang phần tiếp theo để mục tiêu thật sự của ABTest là gì? và thấy được cách mình vừa trình bày ở trên là sai lầm.
Làm rõ mục tiêu của việc ABTest
Chúng ta đã quên mất 2 điều mà khi quên 2 điều này làm cho chúng ta cứ nghĩ rằng mình vẫn đang làm đúng.
- Mục tiêu của việc kiểm định là để chứng minh model cải tiến tốt hơn trên toàn bộ tập khách hàng. Tập khách hàng này là tập khách hàng tại mọi thời điểm, tại tương lai, hiện tại, và quá khứ. Câu phát biểu này phát sinh vấn đề là vậy thì tập khách hàng tương lai ở đâu chứ? Chúng ta chưa có. Vậy thì làm sao để có tập khách hàng tương lai này chứ? chúng ta sẽ chờ cho công này phá sản. Vậy thì toàn bộ tập khách hàng của công ty là từ lúc công ty khởi nghiệp đến lúc phá sản. Lúc này đây, bạn dùng chiến lược ABTest ngây thơ ở trên để tính toán thì bạn làm đúng.
Nhưng mà công ty này phá sản thì ai cần bạn làm gì nữa chứ? Vậy giải pháp là gì?
Chắc chắn rằng chúng ta vẫn phải đạt được mục tiêu là chứng minh rằng model cải tiến tốt hơn trên toàn bộ tập khách hàng, nhưng thay vì phải đợi công ty phá sản để có được toàn bộ tập khách hành, chúng ta sẽ sampling tập khách hàng để đem ra kiểm định, và đó chính là tập khách hàng hiện tại và cũng vì chúng ta sampling một tập nhỏ hơn nên các con số chúng ta tính toán là biến ngẫu nhiên. Vì là biến ngẫu nhiên nên chúng ta có thể thấy chỉ số của mô hình cải tiến tốt hơn, hoặc tệ hơn nhưng không có nghĩa là chúng tốt/tệ hơn thật. Đơn giản chỉ vì ngẫu nhiên!.
Có bạn sẽ thắc mắc, sao lại phải kết luận trên toàn bộ tập khách hàng cơ chứ!. Vậy mình sẽ lấy ví dụ minh họa như sau.
Bạn chế tạo ra vacxin Pfizer để ngừa COVID-19. Và một số người lanh lợi sẽ hỏi rằng, vacxin này có thể giảm tỉ lệ tử vong bao nhiêu cho người được tiêm, những người này có thể là bây giờ, hoặc sau 1 năm nữa. Bạn phải kết luận cho tập người sau 1 năm nữa tiêm vacxin cũng phải có hiệu quả chứ? không lẽ bạn chỉ kết luận cho tập người được tiêm trong năm nay không thôi sao? Nhỡ đâu tập người tiêm 1 năm sau bị biến chứng nặng hơn sau khi tiêm vacxin thì sao? Đó là lý do tại sao chúng ta cần kết luận trên toàn bộ quần thể (population), toàn bộ tập khách hàng.
Và để trả lời cho tại sao Chiến lược ABTest ngây thơ là sai thì đó là việc bạn chỉ đơn giản tính các chỉ số trên tập sampling rồi so sánh 2 số đó như là 2 biến bình thường thì bạn chỉ kết luận được trên tập sampling đó mà thôi. Ko trả lời được liệu trên toàn bộ population có tốt hơn thật hay không?
Các khái niệm về xác suất cơ bản liên quan đến A/B Testing
Phần này giới thiệu một số khái niệm về xác suất thống kê để làm vững chắc nền tảng cho bạn đọc.
Random process
Các bạn có thể suy nghĩ random process là một process mà kết quả (outcome) là ngẫu nhiên hay chứ không phải tất định. Một số ví dụ về random process như sau:
- Tung đồng xu
- Tung xúc xắc
- Lắc một hộp chứa các loại viên bi xanh,đỏ, … sau đó bốc một viên mà không được nhìn.
- Sampling ngẫu nhiên tập khách hàng của chúng ta
Biến ngẫu nhiên (random variable)
Có thể tưởng tượng biến ngẫu nhiên là biến phụ thuộc vào quá trình ngẫu nhiên. Ví dụ
- Giá trị của mặt xuất hiện trên xúc xắc khi chúng ta tung xúc xắc.
- Tung 2 con xúc xắc và tính tổng của 2 mặt xuất hiện.
Đến đây, bạn có thể thấy rằng, giá trị conversion rate của tập khách hàng mà chúng ta sampling là biến ngẫu nhiên.
Phân bố xác suất (Probability distribution)
Biến ngẫu nhiên nhận một tập giá trị, do đó nó sẽ có cái mà người ta gọi là phân bố xác suất. Cụ thể, phân bố xác suất cho biết khả năng mà biến ngẫu nhiên nhận giá trị đó là bao nhiêu.
Conversion rate của tập khách hàng mà chúng ta sampling cũng sẽ có phân bố xác suất nhé.
Phân bố xác suất có rất nhiều loại khác nhau, mỗi loại có vài tham số đặc trưng cho phân bố đó.
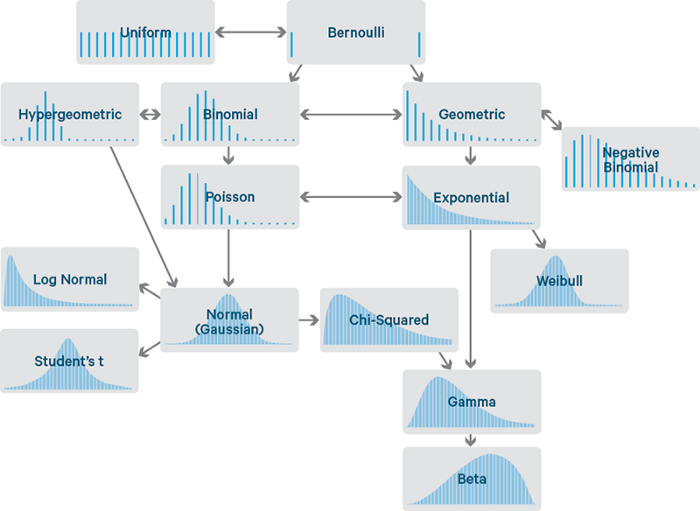 Bức ảnh này thể hiện gia phả của các phân bố xác suất cơ bản
Bức ảnh này thể hiện gia phả của các phân bố xác suất cơ bản
Mình sẽ giải thích vài loại phân bố xác suất phổ biến cơ bản.
Phân bố đều (Uniform Distribution)
Là phân bố mà xác suất xuất hiện của các giá trị mà biến ngẫu nhận được là bằng nhau
Mình họa của phân bố đều trong thực tế mà bạn có thể quan sát được là:
- Phân bố xác suất của biến ngẫu nhiên là giá trị mặt xúc sắc mà bạn quan sát được khi tung con xúc sắc 1 lần.
- hoặc là 1 con bài mà bạn có thể nhận được trong bộ bài 54 lá
Phân bố Bernoulli (Bernoulli Distribution)
Là phân bố rời rạc, trong đó, tập giá trị mà biến ngẫu nhiên có thể nhận được chỉ gồm 2 giá trị Success hoặc Fail. Nếu xác suất của success là p thì xác suất của fail là 1 - p. Thông thường, các câu hỏi dạng yes/no (yes/no question) thuộc phân bố bernoulli. Bernoulli là tên của Jacob Bernoulli người Thụy Sĩ.
Các ví dụ minh họa biến ngẫu nhiên có phân bố Bernoulli là:
- có xuất hiện mặt ngửa khi tung đồng xu 1 lần hay không?
và các ví dụ sau rất phổ biến trong thực tế mà mình gặp phải khi làm việc tại các công ty
- 1 khách hàng có click hay không vào quảng cáo?
- 1 khách hàng có mua sản phẩm hay không?
- 1 khách hàng có kết bạn khi mình gợi ý hay không?
Nên lưu ý rằng mình ghi số lượng là 1 khách hàng click/mua sắm/kết bạn và 1 lần tung đồng xu. Nếu có 2 khách hàng hoặc 2 lần tung đồng xu thì lúc này biến ngẫu nhiên là trạng thái 2 khách hàng không còn là phân bố bernoulli nữa vì các giá trị mà biến ngẫu nhiên này nhận được là 4 giá trị khác nhau. Lúc này, biến ngẫu nhiên trạng thái 2 khách hàng thuộc phân bố nhị thức ở dưới nhé.
Phân bố nhị thức (Binomial distribution)
Mình nghĩ là bắt đầu với một ví dụ để các bạn thấy sự khác biệt do của phân bố nhị thức với phân bố bernoulli mà ta là nói ở trên sẽ đơn giản hơn.
Chúng ta bắt đầu với phân bố nhị thức bằng cách đặt câu hỏi sau:
- 1 khách hàng có click hay không vào sản phẩm mà chúng ta quảng cáo ? sau đó chúng ta lại hỏi thêm câu
- nếu bây giờ chúng ta có 10 khách hàng, vậy số khách hàng click vào quảng cáo sẽ như thế nào?
Câu chúng ta vừa hỏi vậy số khách hàng click vào quảng cáo sẽ như thế nào? có phân bố nhị thức.
Vậy phân bố nhị thức là phân bố của biến ngẫu nhiên mà khi chúng ta hỏi câu có bao nhiêu lần quan sát được success event trong n lần thực hiện thí nghiệm, mỗi lần thí nghiệm là một câu hỏi yes/no question.
Phân bố nhị thức có mối quan hệ tuyệt vời với phân bố chuẩn mà chúng ta sẽ nói đến ở các phân tiếp theo.
Phân bố chuẩn (Normal distribution)
Phân bố này được kí hiệu \(\mathcal{N}(\mu, \sigma^{2})\) và có công thức như dưới đây
Bạn có thể tưởng tượng phân bố chuẩn là phân bố có hình dạng cái chuông (bell curve), đối xứng qua trung tâm. Phân bố này có tính chất là xác suất 1 điểm nằm trong 1std, 2std, 3std (std: là độ lệch chuẩn) tương ứng là 68%, 95% và 99.8%. Tính chất này gọi là quy tắc 68-95-99.7 . Quy tắc này thường dùng để kiểm tra nhẹ nhàng xem một phân bố dạng bell curve có phải là phân bố chuẩn hay không? và không phải phân bố nào đối xứng 2 bên và có hình chuông thì cũng là phân bố chuẩn đâu nhé
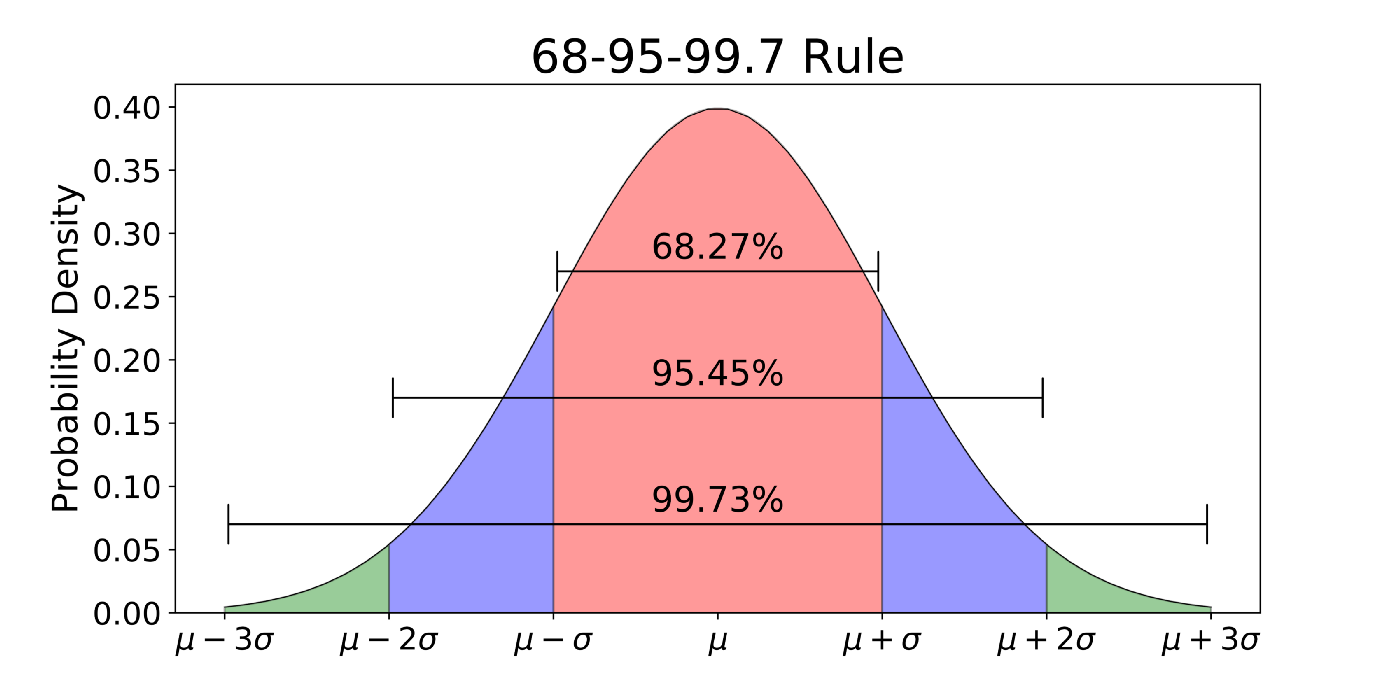 Minh hoạt phân bố chuẩn và quy tắc 68-95-99.7
Minh hoạt phân bố chuẩn và quy tắc 68-95-99.7
Mình nghĩ rằng phân bố chuẩn là phân bố quan trọng nhất trong các loại phân bố bởi vì nó là phân bố phổ biến nhất trong đời sống, lý do phân bố chuẩn lại phổ biến có thể được giải thích bằng central limit theorem mà chúng ta sẽ tìm hiểu ở phần sau nhé.
Một số biến ngẫu nhiên có phân bố chuẩn là:
- Chiều cao của dân số
- Chỉ số IQ
Ngoài ra, khi cộng hoặc nhân \(X \sim N(\mu, \sigma^2)\)với một hằng số C thì ta sẽ có một phân bố chuẩn mới như dưới đây.
Cho \(X \sim N(\mu, \sigma^2)\) thì
- \[X + c \sim N(\mu + c, \sigma^2)\]
- \[c*X \sim N(c\mu, c^2\sigma^2)\]
Z-scores(còn gọi là standard scores) là độ đo cho biết giá trị quan sát bằng bao nhiêu độ lệch chuẩn tính từ trung bình của một phân bố. Thông thường Z-scores hay dùng trong phân bố chuẩn. Z-score được tính như sau: \(z-score = \frac{x - \mu}{\sigma}\) Chúng ta có thể dùng z-score so sánh tương đối giữa 2 điểm dữ liệu mà thuộc 2 phân bố khác nhau. z-score được dùng để tính nhanh p-value.
Mối quan hệ giữa binomial distribution và normal distribution
Các bạn hãy nhớ rằng chúng ta có thể dùng phân phối chuẩn để xấp xỉ phân bố nhị thức khi phân bố nhị thức thỏa điều kiện: xác suất p success gần 0.5 hoặc số lần thí nghiệm n lớn.
Khi p càng lệch về 2 phía (xấp xỉ 1 hoặc 0 ) thì càng cần nhiều lần thí nghiệm hơn để phân bố nhị thức xấp xỉ phân bố chuẩn, hoặc đơn giản ghi nhớ rule này np > 10 và n(1-p)>10
Phát biểu lại như sau \(X \sim B(n, p)\) với n đủ lớn thì X sẽ xấp xỉ \(\mathcal{N}(np, np(1-p))\)
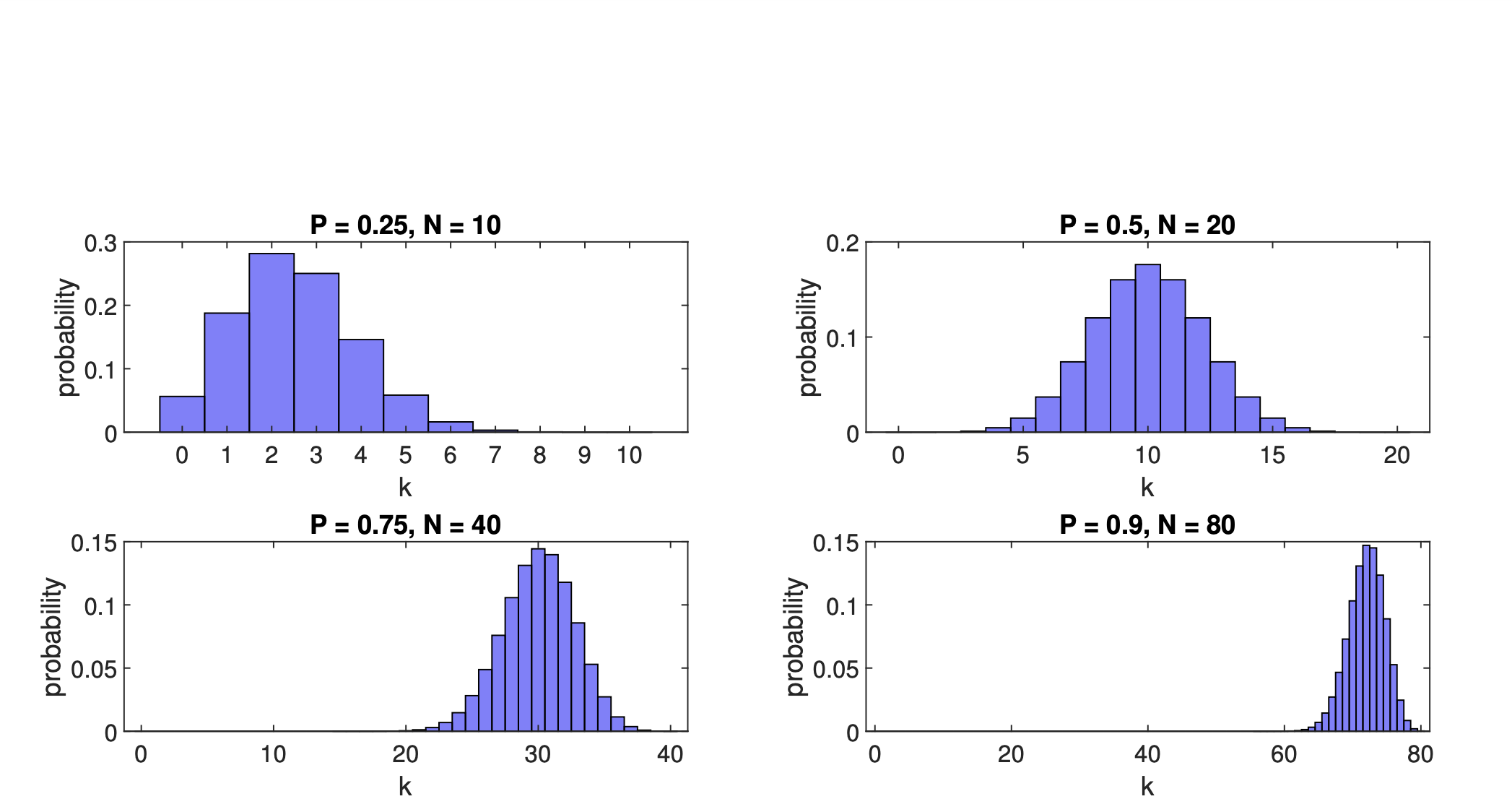 Normal approximation to the Binomial
Normal approximation to the Binomial
Câu hỏi là tại sao chúng ta lại thích xấp xỉ phân bố nhị thức thành phân bố chuẩn làm gì? bởi vì phân bố chuẩn được sử dụng rộng rãi, chúng ta dễ dàng ghi nhớ các tính chất của nó, cũng như z score và p value, nên chúng ta dễ tính nhẩm hơn và công thức được rút gọn đẹp hơn.
Mối quan hệ giữa proportion distribution và binomial distribution
Proportion distribution và binomial distribution có mối quan hệ chặt chẽ với nhau. Nếu \(X \sim B(n, p)\) thì Y=X/n sẽ là proportion distribution. Khi n đủ lớn thì \(Y \sim N(p, p(1-p)/n)\). Mình nói đến proportion distribution là bởi vì khi chạy ABTest chúng ta thường tính tỉ lệ conversion rate, tỉ lệ này chính là proportion distribution, nếu chúng ta biết được phân bố của nó thì sẽ đơn giản tính được z_score và p_value. Dựa vào p_value là chúng ta kết luận được version B có tốt hơn A hay không?
Các điều quan trọng khi làm ABTest
AB testing chia ngẫu nhiên user thành 2 tập có kích thước tương đương nhau:
- control: tập mặc định trước khi áp dụng mô hình cải tiến
- variant: tập áp dụng mô hình cải tiến.
Sử dụng kiểm định giả thuyết để so sánh chỉ số cần quan tâm trên 2 tập trên, và từ đó quyết định xem có nên áp dụng mô hình cải tiện hay không?
Có 3 điểm cần lưu ý khi làm ABTest.
- Cần chia user thành 2 tập ngẫu nhiên. Việc chia ngẫu nhiên làm cho các tác động khác (ngoại trừ cải tiến mà chúng ta định áp dụng cho tâp control) phân bố đều vô 2 tập. Từ đó đảm bảo không có bias khi chúng ta thực hiện thí nghiệm.
- 2 tập user không cần có kích thước giống nhau, tuy nhiên mình khuyến khị nên số lượng bằng nhau, điều này giúp chúng ta tiết kiệm thời gian chạy test hơn là khi chia tập user không đều nhau.
- và điều quan trọng nhất đó là so sánh các chỉ số bằng
kiểm định giả thuyết. Do chúng ta so sánh các chỉ số có tính ngẫu nhiên như phân tích ở trên, nên không thể nào so sánh kiểu tuyệt đối như 2 > 1… mà chúng ta phải so sánh phân bố của các giá trị mà biến ngẫu nhiên có thể nhận được.
Có nhiều tài liệu tham khảo trên internet nói về ABtest nhưng họ lại không đề cập việc phải dùng kiểm định giả thuyết để so sánh các chỉ số do đó thường gây ra hiểu lầm cho rất nhiều người. Ở phần tiếp theo, mình sẽ trình bày chi tiết cách sử dụng kiểm định giả thuyết trong ABTest như thế nào.
Chúng ta có thể so sánh 2 biến ngẫu nhiên như thế ?
Khi 2 biến ngẫu nhiên có cùng ý nghĩa, mình nghĩ rằng chúng ta có thể dùng ý tưởng sau đây để so sánh 2 phân bố của biến ngẫu nhiên rời rạc để từ đó kết luận biến ngẫu nhiên x có lớn hơn y hay không?. Cụ thể hơn là
- Chúng ta có thể nói x > y khi các giá trị mà x nhận được lớn hơn tất cả các giá trị mà y nhận được.
- Chúng ta có thể nói x < y khi các giá trị x nhận được bé hơn tất cả các giá trị y nhận được.
Sự nhọc nhằn trong cách tính conversion rate trong thực tế.
Có thể chúng ta đã hiểu được cần chia tập khách hàng thành 2 tập a,b ngẫu nhiên bằng nhau, chúng ta cũng hiểu cần so sánh 2 biến ngẫu nhiên dựa vào phân bố của chúng chứ không phải so sánh giá trị tuyệt đối. Nhưng mà đến lúc này, chúng ta vẫn có thể vẫn mắc một sai lầm nữa là chúng ta lại đi cân đo đong đếm 2 biến ngẫu nhiên mà kết quả việc này lại không trả lời chính xác được câu hỏi của business. Lý dó là thứ nhất câu hỏi của business lỏng lẻo, thứ 2 là chúng ta tính toán không chuẩn xác.
Ví dụ dưới này sẽ làm cho các bạn dễ hình dung
Vào một ngày đẹp trời, có một bạn team business muốn chúng ta cải thiện giao diện hiển thị sản phẩm để tăng tỉ lệ conversion khi user mua hàng? Vậy thì câu hỏi đầu tiên xuất hiện trong đầu chúng ta là? tỉ lệ conversion của user khi mua hàng được định lượng như thế nào? Chúng ta sẽ nhiều cách
- số lượng user click add_to_cart / số lượng user vào trang sản phẩm
- số lượng user click add_to_cart / số lượng user đã vào trang landing page
- số lượng user thực hiện thành công thanh toán / số lượng user vào trang sản phẩm
- số lần hiển thị sản phẩm có lượt mua / số lần hiển thị sản phẩm (một lần refresh page là 1 lần hiển thị)
- và nhiều cách tính khác.
Cách đúng có lẽ phụ thuộc vào việc bạn hiểu business và hiểu những rủi ro trong các các tính khác nhau.
Chọn success event
Vậy thì trước khi bắt đầu ABTest cho những đại lượng là tỉ lệ thì chúng ta cần xác định được success event là gì trước nhất, tuy nhiên việc chọn success event cũng khá là không rõ ràng, vì có nhiều cách tính cho cùng một khái niệm như đã nói ở trên, và hơn nữa vì có nhiều cách tính cho cùng một khái niệm nên kết quả từ việc so sánh các chỉ số đó lại mâu thuẫn với nhau. ví dụ, bạn muốn chọn một chỉ số để đo performance của widget mới trên website TIKI, chúng ta bịa… ra 2 chỉ số sau.
- tỉ lệ A = user click/tỉ lệ user view
- tỉ lệ B = user mua hàng / tỉ lệ user view
nếu cả 2 chỉ số cùng tốt , hoặc cùng tệ hơn thì không có gì để bàn cãi. Tuy nhiên, nếu chỉ 1 trong 2 chỉ số tốt hơn, thì chúng ta bắt đầu gian lận bằng cách, chọn tỉ lệ nào lớn hơn thì lấy cái đó làm success event, rồi tuyên bố cái cái version mới mà chúng ta đang bỏ công sức vào làm là tốt hơn. Chọn như nào là tốt là câu hỏi mà mình còn chưa có câu trả lời, tuy nhiên, mình vẫn nghĩ tốt nhất là nên chọn chỉ số là key metric để tối ưu theo chỉ số đó, nếu không thì chúng ta sẽ nhảy tới, nhảy lui mà không thật sự cải thiện được gì cả.
Hypothesis testing
Sau khi, chúng ta thu thập đủ dữ liệu bằng việc đợi cho thí nghiệm của chúng ta hoàn thành.
Cách kiểm định ngây thơ
Chúng ta biết ý tưởng của việc so sánh chỉ số của 2 tập A và B đó là so sánh 2 phân bố của chỉ số này. Đến lúc này, chúng ta lại hỏi, chúng ta chỉ thực hiện một lần thí nghiệm trong n ngày thôi thì lấy đâu ra nguyên cái phân bố để so sánh chứ? Cách dễ nhất là… cứ thực hiện thêm m lần nữa là được mà :) Trong thực tế thì việc này khá tốn công sức, thay vào đó, chúng ta sử dụng một sử dụng ý tưởng kiểu như: giả sử phân bố của tập control là phân bố đúng, vậy thì dữ liệu chúng ta quan sát thấy trong thí nghiệm có xác suất bao nhiêu, nếu xác suất đó hiếm thì chúng ta có thể đưa ra một số kết luận. Idea mình vừa nói chính là ý tưởng tổng quan của hypothesis testing.
Do đó phần dưới này là lý thuyết trình bày cách so sánh chỉ số trên tập A và B với hypothesis testing. Ý tưởng chung của hypothesis testing là tính p_value, cái mà được định nghĩa là xác suất chúng ta quan sát được sự kiện trong thí nghiệm dưới trường hợp giả thiết H_null là chính xác.
Tuy nhiên trước khi đi vào giới thiệu 2 kiểm định giả thiết phổ biến, mình sẽ nhắc lại định lý giới hạn trung tâm, một trong những định lý cốt lõi của lý thuyết thống kê.
Central Limit Theorem
Phát biểu cơ bản của định lý CLT như sau: Cho \(X_{1}, X_{2},... X_{n}\) là các random sample của n lần thử độc lập thuộc phân bố có kì vọng \(\mu\) và variance hữu hạn \(\sigma^{2}\), thì khi \(n \to \infty\) vô cùng,
với \(\bar{X}_{n} = \frac{X_{1} + ... + X_{n} }{n}\)
 Minh hoạ CLT
Minh hoạ CLT
Để dễ hiểu hơn, bạn hãy tưởng tượng đang chơi một trò chơi trong đó bạn tung một con xúc xắc có sáu mặt thường. Mỗi lần bạn tung nó, bạn nhận được một số từ 1 đến 6. Bây giờ, hãy nói rằng bạn chỉ tung xúc xắc một lần duy nhất. Bạn có thể nhận được bất kỳ số nào từ 1 đến 6 và điều đó là bình thường.
Nhưng bây giờ, hãy tưởng tượng bạn tung xúc xắc rất nhiều lần, như cả trăm lần hoặc thậm chí nhiều lần hơn. Mỗi lần bạn tung, bạn ghi lại số mà bạn nhận được. Sau khi bạn đã tung xúc xắc nhiều lần, bạn sẽ có một loạt các số đã được ghi lại.
Bây giờ, nếu bạn nhìn vào tất cả những số đó và tìm ra trung bình (bạn cộng tất cả các số lại và sau đó chia cho số lần bạn đã tung xúc xắc), một điều thú vị xảy ra. Bất kể những con số trông như thế nào khi bạn tung xúc xắc mỗi lần, trung bình của tất cả những con số đó sẽ bắt đầu trông giống như một số đặc biệt: số 3.5.
Điều này có phần giống như ma thuật! Ngay cả khi mỗi lần tung xúc xắc đều cho bạn các số khác nhau, khi bạn nhìn vào trung bình của tất cả những lần tung, nó sẽ ngày càng tiến gần hơn đến 3.5 khi bạn thực hiện nhiều lần tung hơn. Mánh khóe ma thuật này được gọi là Định lý Giới hạn Trung tâm.
Vậy nên, Định lý Giới hạn Trung tâm nói cho chúng ta biết rằng khi chúng ta thực hiện một việc gì đó nhiều, nhiều lần và nhìn vào trung bình của những gì xảy ra, thường thì nó sẽ trở nên rất dễ đoán, ngay cả khi các sự việc cá nhân không thể đoán trước được chút nào. Điều này giống như khi bạn kết hợp nhiều màu sắc của đất nặn - càng kết hợp nhiều, bạn càng tiến gần tới một màu cụ thể.
CLT quan trọng bởi vì nó cho phép chúng ta inference about population based on a sample bằng phát biểu distribution sample mean sẽ xấp xỉ normal distribution khi sample size lớn bất kể phân bố gốc là gì, bên cạnh đó nhiều phương pháp kiểm định giả thuyết đều dựa vào tính normality của dữ liệu.
Quy trình thực hiện hypothesis testing:
Kiểm định giả thuyết (Hypothesis testing) là một phương pháp trong thống kê dùng để đưa ra quyết định về một giả thuyết về dữ liệu dựa trên dữ liệu mẫu. Quá trình này giúp bạn xác định xem liệu có đủ bằng chứng để bác bỏ giả thuyết ban đầu hay không. Cách thực hiện kiểm định giả thuyết thường bao gồm các bước sau:
-
Xác định giả thuyết:
- Giả thuyết không (null hypothesis - H0): Đây là giả thuyết ban đầu, thường khẳng định rằng không có sự khác biệt hoặc không có hiệu ứng đáng kể. Ví dụ: Giá trị trung bình bằng một giá trị đã biết trước.
- Giả thuyết thay thế (alternative hypothesis - H1): Đây là giả thuyết mà bạn muốn kiểm tra, thường khẳng định rằng có sự khác biệt hoặc có hiệu ứng đáng kể. Ví dụ: Giá trị trung bình không bằng giá trị đã biết trước.
-
Chọn mức ý nghĩa (significance level - α): Đây là ngưỡng quyết định để xác định liệu bạn sẽ bác bỏ giả thuyết không hay không. Mức ý nghĩa thường được chọn là 0.05 (5%), nhưng bạn có thể chọn mức khác tùy theo nghiên cứu của bạn. Lý do, mọi người hay chọn p_value=0.05 có thể là do giá trị 0.05 được chọn bởi Fisher ( người được coi là cha đẻ của thống kê hiện đại). Ông đã thuyết trình và đơn giản là đưa ra giá trị 0.05 là ngưỡng để phân biệt một với kiện hiếm có đến mức có thể không phải chỉ do ngẫu nhiên mà còn do những yếu tố khác. Liệu có giá trị p=0.051 có khác biệt nhiều so với 0.0499 hay không?. Câu trả lời là không. Cuộc sống có nhiều sắc thái xám, và đôi khi chúng ta phải đưa ra quyết định có/không và chúng ta phải chọn một đường chia ở đâu đó. Liệu một bác sĩ có quyết định cho bệnh nhân dùng thuốc mới hay không, một không cty có nên chấp nhận thay đổi mới hay không? Đôi khi, bạn phải chọn. Vậy đó!

-
Thu thập và xử lý dữ liệu: Thu thập dữ liệu từ tập mẫu và tiến hành các phép tính cần thiết như tính trung bình mẫu, độ lệch chuẩn, tỷ lệ, v.v.
-
Chọn kiểu kiểm định (one-tailed hoặc two-tailed): Tùy theo câu hỏi nghiên cứu và giả thuyết, bạn chọn kiểu kiểm định một chiều (one-tailed) hoặc hai chiều (two-tailed). Kiểm định một chiều tập trung vào một hướng khác biệt (lớn hơn hoặc nhỏ hơn), trong khi kiểm định hai chiều tập trung vào sự khác biệt tổng quát. Thông thường trong ABTest, chúng ta kiểm định một chiều tập variant có performance tốt hơn so với tập baseline hay không?
-
Tính toán giá trị thống kê: Dựa trên dữ liệu mẫu và giả thuyết, tính giá trị thống kê cụ thể cho phương pháp kiểm định bạn sử dụng (như Z-score, t-score, chi-square, v.v.).
-
Tính giá trị p (p-value): Giá trị p đo lường xác suất tìm thấy kết quả mẫu hoặc kết quả cận biên (critical value) trong vùng từ chối dưới giả thuyết không. Tính giá trị p dựa trên giá trị thống kê và phân phối xác suất.
-
So sánh giá trị p và mức ý nghĩa: Nếu giá trị p nhỏ hơn hoặc bằng mức ý nghĩa, bạn có thể bác bỏ giả thuyết không. Nếu giá trị p lớn hơn mức ý nghĩa, bạn không có đủ bằng chứng để bác bỏ giả thuyết không.
-
Đưa ra kết luận: Dựa trên quyết định đã ra, bạn có thể kết luận về giả thuyết ban đầu và sự khác biệt dựa trên dữ liệu mẫu.
Một số khái niệm liên quan cần biết trước khi thiết kế ABTest
Minimum Detectable Effect
Minimum Detectable Effect (MDE) liên quan đến việc xác định số lượng user cần thiết để có thể detect được improvement. Ví dụ, chúng ta muốn cái test hiện tại có thể xác định được 2% relative improvement so với tập baseline với tham số p_value=0.05 và power=0.8 thì cần tối thiếu số lượng bao nhiêu để có thế detect được
Công thức tính số lượng user tối thiểu phụ thuộc vào significant level
Statistical Power
Power là xác suất mà chúng ta xác định có real effect trong thí nghiệm đang chạy. Ví dụ power=80% có nghĩa là chúng ta mong muốn test đang chạy sẽ statistical significant nếu bản variant thực sự có sự cải thiện.
P_value
P_value (probability value) là xác suất chúng ta thu được kết quả kiểm tra ít nhất bằng cái test result của tập variant dưới điều kiện giả thuyết không đúng.
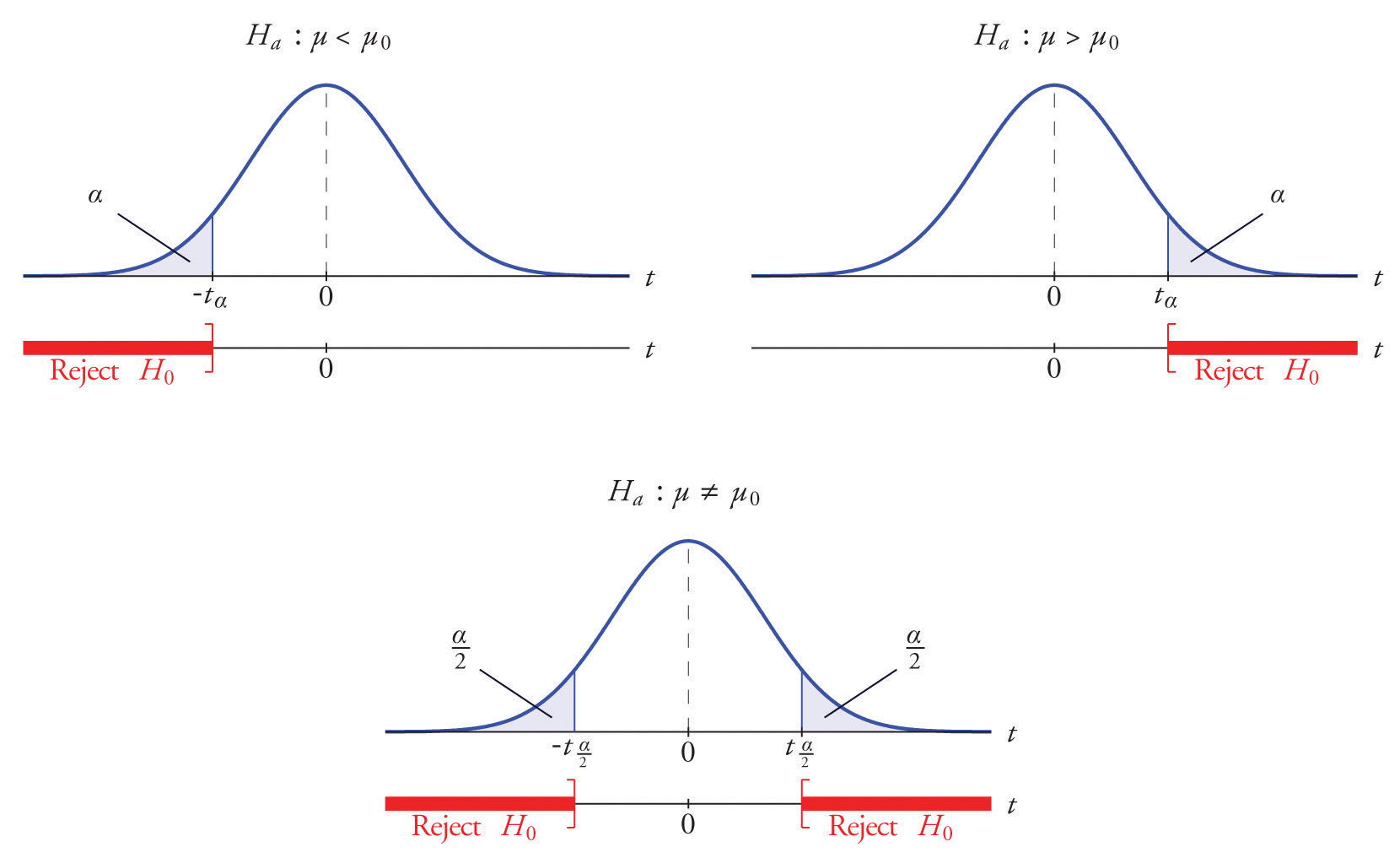 Minh hoặc p_value cho left tailed test, right tailed test và 2 sided test
Minh hoặc p_value cho left tailed test, right tailed test và 2 sided test
Tính p_value cho kiểm định tỉ lệ.
Ví dụ TIKI muốn kiểm tra giao diện mới có tỉ lệ user mua hàng cao hơn hay không? … dựa vào từ tỉ lệ chúng ta biết ngay là dùng kiểm định giả thuyết của propotion rồi đó. Vậy chúng ta xây dựng 2 giả thuyết cho bài này như sau:
- Giải thuyết không \(H_{0}\): Tỉ lệ của sự kiện của tập baseline và variant bằng nhau.
- Giải thuyết thay thế \(H_{a}\): Tỉ lệ của sự kiện tập variant lớn hơn trong tập baseline. Và chúng ta tính z_score như sau: khi n đủ lớn thì tỉ lệ của sự kiện có phân bố chuẩn với kì vọng \(\mu=p_0\) và độ lệch chuẩn \(\sigma = \sqrt{\frac{p_0(1-p_0)}{n}}\). Do đó z_score = \(\frac{(\widehat{p} - p_{0})}{\sqrt{\frac{p_0(1-p_0)}{n}}}\).
Trong đó \(p_0\) là tỉ lệ trong tập baseline, n là kích thước tập baseline, \(\widehat{p}\) là tỉ lệ trong tập variant.
Tính p_value cho kiểm định trung bình.
Ví dụ TIKI muốn kiểm định xem chương trình mua kèm giảm thêm có thực sự tăng giá trị đơn hàng mà khách hàng mua hay không? Lúc đó, chúng ta muốn chạy kiểm định giả thiết trung bình để xem tập variant có giá trị đơn hàng trung bình lớn hơn tập baseline hay không?
- Giải thuyết không \(H_{0}\): Trung bình giá trị đơn hàng của tập baseline và variant bằng nhau.
- Giải thuyết thay thế \(H_{a}\): Trung bình giá trị đơn hàng của tập variant lớn hơn tập baseline.
Chúng ta tính z_score như sau: khi n đủ lớn thì trung bình giá trị đơn hàng có phân bố chuẩn với kì vọng \(\mu\) và độ lệch chuẩn \(\frac{\sigma}{\sqrt{n}}\). Do đó, z_score = \(\frac{\widehat{X} - \mu_{0}}{\frac{\sigma}{\sqrt(n}}\). Trong đó
- \(\widehat{X}\): là trung bình tập variant
- \(\mu_{0}\): trung bình tập baseline, \(\sigma\): độ lệch chuẩn tập baseline, \(n\): kích thước mẫu. Dựa vào z_score để tính p_value để đưa ra kết luận.
Hiện tại, mình sẽ kết thúc bài viết về ABTest ở đây, với kiến thức hạn hẹn của một engineer, mình hy vọng sẽ đón nhận các feedback để sửa lại bài viết tốt hơn. Các topics ở dưới sẽ không được cover trong bài viết này, tuy nhiên mình sẽ liệt kê ở đây để bạn có thể tự tìm hiểu thêm.
ABTest khi không biết phân bố của biến ngẫu nhiên
Tính prob của (B tốt hơn A)
Bayesian hypothesis testing là gì?
How to use hypothesis testing to lie
Một số quan điểm sai lầm
- Saying “We accept the Null hypothesis”: You either reject the null hypothesis or fail to reject the null hypothesis.
Tham khảo
- https://math.stackexchange.com/questions/845769/why-does-the-normalized-z-score-introduce-a-square-root-and-some-more-confusio
(1): (Phần này mình không hiểu rõ, chỉ muốn đưa ra một số ví dụ cho mọi người có cái nhìn thêm)
